최적화와 경사하강법(Gradient Descent)
1. 손실 함수(loss function)의 최적화(Optimization)
최적화란 일상에서 우리가 익숙하게 경험하고 있는 원리다. 집에서 직장까지의 최단 경로를 고려해서 출퇴근을 하거나, 여행 계획을 짤 때 시간과 비용을 고려해서 최적의 장소를 선별하는 등 일상에서 우리는 수많은 최적화 과정을 거친다.
머신러닝 분야에서 최적화(Optimization)는 손실 함수(loss function)을 최소화하는 파라미터를 구하는 과정을 말한다. 손실 함수는 지도학습(Supervised Learning) 시 알고리즘이 예측한 값과 실제 정답의 차이를 비교하기 위한 함수이다. 즉, '학습 중에 알고리즘이 얼마나 엉터리인지를 측정하는 기준'를 확인하기 위한 함수로써 최적화를 위해 최소화하는 것이 목적인 함수이다.
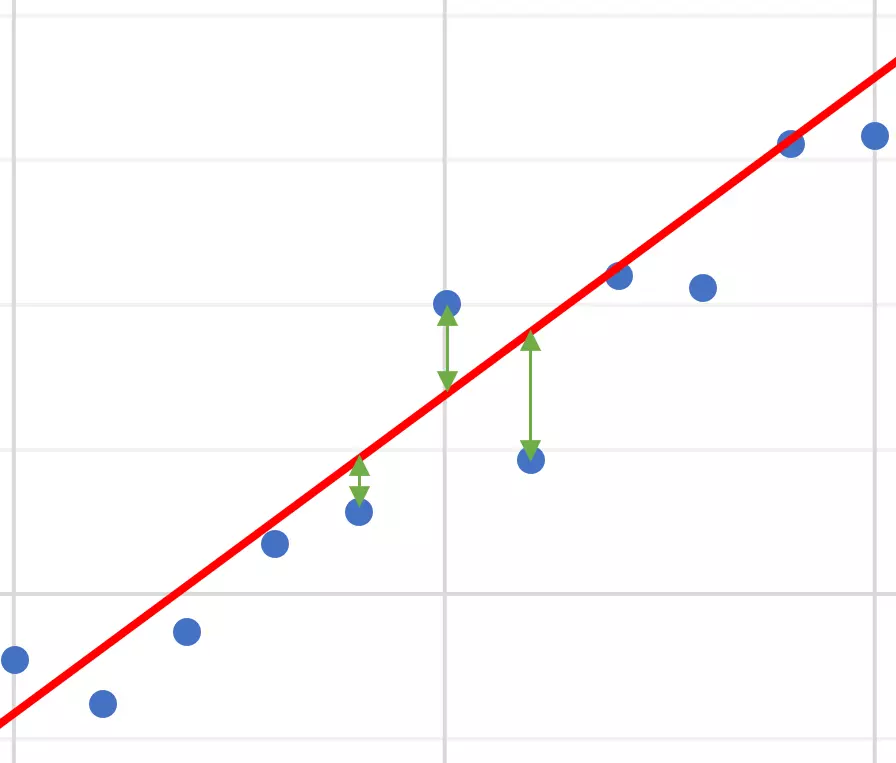
대표적인 손실함수로는 로지스틱 손실함수(logistic loss function, binary cross-entropy loss function)와 mse가 있다. 손실함수에 대해서는 추후 포스팅 예정이다(아마).
✅ 손실 함수와 비용 함수
비용 함수(cost function)은 손실 함수의 다른 말이다. 엄밀히 말하면 손실 함수는 샘플 하나(표본)에 대한 손실을 정의하고, 비용 함수는 모든 샘플(모집단)에 대한 손실 함수의 합을 말한다. 그러나 보통 이 둘을 엄격히 구분하지 않고 섞어서 사용한다.
2. 경사하강법(Gradient Descent)
1) 정의
이제 파라미터를 결정하기 위해 손실함수를 최소화하는 방법이 바로 경사하강법(Gradient Descent)이다. 기본 개념은 함수의 기울기(경사)를 구하고 경사의 반대 방향으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것이다(위키백과).경사하강법은 다음과 같이 많이 비유되기도 한다.
앞이 보이지 않는 안개가 낀 산을 내려올 때는 모든 방향으로 산을 더듬어가며 산의 높이가 가장 낮아지는 방향으로 한 발씩 내딛어갈 수 있다.
2) 미분계수를 쓰지 않는 이유
함수의 최솟값을 찾으려면 “미분계수가 0인 지점을 찾으면 되지 않느냐?”라고 물을 수 있는데, 미분계수가 0인 지점을 찾는 방식이 아닌 gradient descent를 이용해 함수의 최소값을 찾는 주된 이유는 아래와 같다.
- 우리가 주로 실제 분석에서 마주하게 되는 되는 함수들은 닫힌 형태(closed form)가 아니거나 함수의 형태가 복잡해 (가령, 비선형함수) 미분계수와 그 근을 계산하기 어려운 경우가 많다.
- 실제 미분계수를 계산하는 과정을 컴퓨터로 구현하는 것에 비해 gradient descent는 컴퓨터로 비교적 쉽게 구현할 수 있기 때문이다.
- Saddle Point (말안장점; 미분해서 0이 된다고 해서 무조건 최적점이 아닐 수 있다)

✅ Saddle Point (말안장점)
가로축을 편의상 Axis1, 세로축을 편의상 Axis2로 놓고 생각해보자. 가운데 빨간 지점을 A라고 칭한다. Axis2를 없애고 (Axis2를 찌그러뜨린다고 생각) Axis1에 대해서 보면 곡면은 아래로 볼록한 포물선의 형태(A: 최소점)를 보일 것이다. Axis1을 없애고 Axis2에 대해서만 본다면 곡면은 위로 볼록한 포물선의 형태(A: 최대점)를 보일 것이다.
가운데 점 A는 Gradient(쉽게 말하면 미분값)는 0이지만 어떻게 보느냐에 최대점, 혹은 최소점이 될 수 있다. 따라서 우리는 미분해서 0이 된다고 해서 이곳이 Globally optimal (전역 최적) 하다고 단정 지을 수 없다. 이때 A는 말안장처럼 생겼다고 하여 말안장점(Saddle Point)이라고 부른다.
- 출처: https://daebaq27.tistory.com/35

3) 경사하강법의 원리
경사하강법은 함수의 기울기(경사, gradient)를 이용해 x의 값을 어디로 옮겼을 때 함수가 최소값을 찾는지 알아보는 방법이라고 할 수 있다.
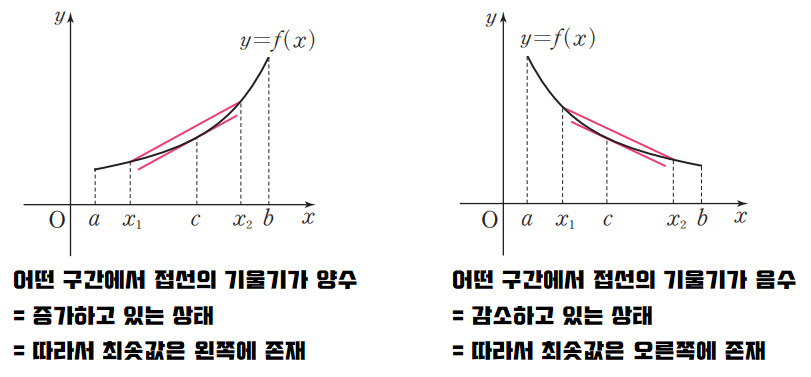
만약 함수의 접선의 기울기의 값이 양수인지 음수인지 알 수 있다고 가정하자.
x=a에서의 접선의 기울기가 양수라면 그 시점에서 함수는 증가하는 상태를 말한다. 즉 x 값이 커질 수록 함수 값이 커진다는 것을 의미하고, 따라서 최솟값은 a보다 작은 쪽인 왼쪽에 존재할 것이다. 반대로 x=a에서의 접선의 기울기가 음수라면 함수는 감소하는 상태를 말한다. 즉, 반대로 기울기가 음수라면 x값이 커질 수록 함수의 값이 작아진다는 것을 의미한다고 볼 수 있으며 최솟값은 a보다 큰 쪽에 위치한다는 것을 의미한다.
동시에 기울기의 값이 크다는 것은 가파르다는 것을 의미하기도 하지만, 또 한편으로는 x의 위치가 최솟값에 해당되는 x 좌표로부터 멀리 떨어져 있는 것을 의미한다.
따라서 접선의 기울기의 부호와 크기에 따라 (엄밀하게는 접선 벡터를 다룸) 최솟값을 가지는 위치를 찾아가는 방법이 바로 경사하강법이다.

이때 얼마의 속도로 최솟값에 다가갈지에 대한 문제가 생긴다. 물론 그 속도는 상황에 따라 다를 수 있다. 최솟값이라는 목적지를 향해 갈수록 기울기는 그 값이 점점 작아지고 그에 비례해서 속도도 작아진다. 접선의 기울기에 얼마의 크기로 비례하여 속도를 내는지를 결정짓는 값이 바로 '학습률(learning rate)'이며 이동거리가 크고 작아진다는 의미에서 step size라고도 부른다.
사용자가 학습률을 어떻게 조절함에 따라 경사하강법의 성능이 달라진다. 이때의 학습률을 α로 쓸 때 다음과 같은 수식을 도출할 수 있다.
4) 최종수식
$x_{i+1} = x_i - \alpha \frac{df}{dx}(x_i)$
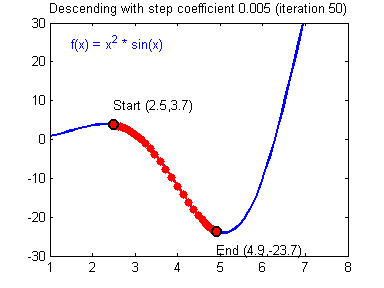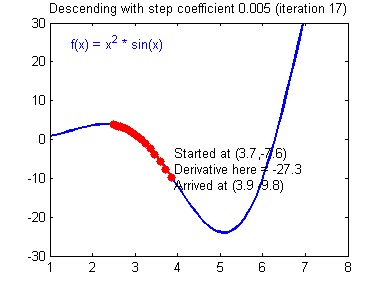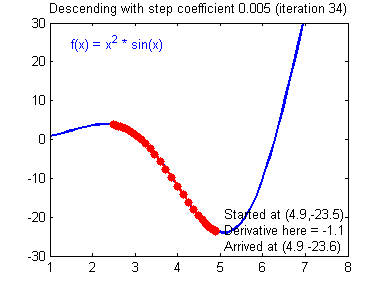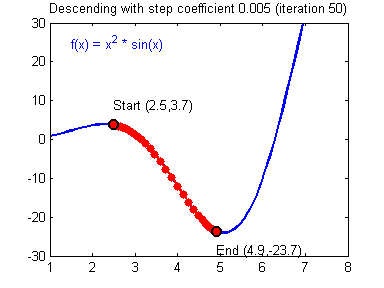
이를 다변수함수에 대해 확장하면 다음과 같이 쓸 수 있다.
$x_{i+1} = x_i - \alpha \nabla f(x_i)$
Q. 왜 gradient 값을 빼줄까? : 손실 함수의 최솟값을 찾아야 하기 때문
식을 보면 그래디언트 값을 빼주는 것을 알 수 있다. 왜 그 값을 빼주는지는 경사하강법이라는 명칭과 관련이 있다. 경사하강법은 기본적으로 목적 함수 최소화에 사용된다. 따라서 Gradient가 양의 값을 갖는다면 현재 파라미터를 변수로 하는 목적 함수가 증가하고 있다는 의미이므로 parameter를 더 작은 쪽으로 움직여야 한다. 반대로 Gradient가 음의 값을 갖는다면, parameter를 더 큰 쪽으로 움직여야 할 것이다. 이에 Gradient에 learning rate(학습률, step size라고도 한다. 어느 정도 이동할 것인지를 정의함)에 곱하여 현재 파라미터 값에서 빼주는 형태로 업데이트 하는 것이다.
반대로 목적 함수를 최대화하는 문제라면, Gradient값을 빼는 것이 아니라 더해주면 될 것이다. 그러나 최대화 문제는 최소화 문제에서 목적함수의 부호만 바꾸는 것으로 간단히 해결할 수 있으므로 Gradient를 더해주는 방향으로 알고리즘 상 변화를 줄 필요는 없다.
- 출처: https://daebaq27.tistory.com/35
5) 학습률(learning rate, step size)
최적화 과정에서 학습률을 설정하여 속도를 결정한다. 정해진 학습률에 따라 계속해서 계산이 이루어지고 어느 순간 그 값이 거의 변화가 없는 수렴하는 구간에 도착한다. 이때의 극한값이 손실함수의 최솟값이면 좋겠으나 항상 그렇지는 않으며 심지어는 수렴하지 않을수도 있다.
학습률이 너무 크면 한 지점으로 수렴하는 것이 아니라 발산할 가능성이 존재하며, 너무 작은 학습률을 선택하면 수렴이 늦어진다. 또한 시작점을 어디로 잡느냐에 따라 수렴지점이 달라질 우려가 있다. 이때가 수렴 지점이 전역 최솟값(global minimum)이 아니라 국소 최솟값(local minima)에 빠진 경우이다.


이처럼 경사하강법은 학습률과 전역 최솟값의 문제를 가지고 있다. 이러한 문제를 해결하기 위해 Momentum, RMSProp, Adam 등의 다양한 최적화 방법이 발전되고 있다.

6) 종류 ⇒ 자세한 건 여기서 참고
- 배치 경사하강법
- 확률적 경사하강법
- 미니배치 경사하강법
Reference
'AI > ML' 카테고리의 다른 글
| Confusion Matrix과 Accuracy (0) | 2022.11.24 |
|---|---|
| PyCaret을 이용한 AutoML Tutorial (0) | 2022.11.17 |
| 정규분포와 Feature Scaling (1) | 2022.11.10 |
| [유튜브 강의록] 04-1: Ensemble Learning - Overview (0) | 2022.11.06 |
| [HML2] Decision Tree와 화이트박스 (0) | 2022.11.03 |




댓글