본 내용은 K-MOOC 실습으로 배우는 머신러닝 강의의 내용을 듣고 작성하였습니다.
실습으로 배우는 머신러닝
www.kmooc.kr
3. Classification
1) 머신러닝 분류 모델링
A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P if its performance at tasks in T, as measured by P, improves with experience E. - Tom Mitchell
과거에는 input을 넣었을 때 output이 나오는 일련의 logic 또는 function, pattern을 사람이 직접 입력해줬다면, 현재의 머신러닝에서는 데이터를 통해 학습한다는게 가장 중요한 개념이다.

머신러닝은 문제 상황(task)에 따라 Supervised Learning, Unsupervised Learning, Reinforcement Learning로 크게 3가지로 분류 가능하다. 먼저 Supervised Learning은 이 이름에서도 알 수 있듯이 모형에게 '이러이러한 input이 들어오면 이런 output이 나와야 돼.’라는 걸 정확하게 알려주는 것이고, 그 안에는 크게 Classification과 Regression, 2가지로 나눠진다.
두 번째는 Unsupervised Learning으로 지도가 되지 않는, 컴퓨터 스스로 데이터에 있는 속성들, 특징들을 추출해내는 그런 작업들을 하는 learning 방법이다. 여기서는 사람이 어떤 레이블이나 사전에 정의된 target response을 가지고서 학습하는 것이 아니라, 그 데이터 자체에 속해 있는 속성들을 찾아내는 방법이다. 강의 중반부에 가서 Clustering에 대해서도 배우고 아니면 이상치, ‘우리가 갖고 있는 데이터랑 많이 다른 그런 애다.’라는 걸 찾아내는 Anomaly Detection도 있다.
마지막으로 강화학습이 있다. 컴퓨터에게 정확히 direction은 주지 않지만 컴퓨터가 취한 액션에 대해서 그거를 잘 했다, 못했다 리워드를 정보로 줌으로써 학습을 하는 방법이다.
이렇게 크게 세 가지가 있고, 본 강의에서는 주로 Supervised Learning 배우며, 2 ~ 3장이 지나서 Unsupervised Learning에 대해서도 배울 것이다. Reinforcement Learning은 advanced된 내용이기 때문에 이 내용을 다 배운 다음 진행 학습하면 될 것 같다. 오늘은 특히 그 중에서 Classification 내용에 대해서 집중적으로 배워보는 시간 갖는다.


Training 상황에서 보지 않았던 데이터를 예측하고 분류하는 과정들이 중요하기 때문에 꼭 이 Testing dataset의 성능을 봐야 된다. 추가로 Training 과정에서조절해야 되는 Hyperparameter가 있었다. 어떤 함수의 특성을 결정지어주는, 기저가 되는 기저함수. 영어로는 basis function의 특징들, 복잡도를 결정해주는 그런 Hyperparameter들이 있었고, 그런 Hyperparameter를 잘 Tuning을 해야 한다.
Hyperparameter의 튜닝은 Training dataset을 다시 또 쪼개서 Validation dataset을 두고서 그 dataset에 대해서 테스트를 해보면서 결정한다. 그 다음에 최적의 Hyperparameter가 결정이 되고 최종적인 기저함수의 기초적인 형태가 구성이 완료되면 그때 Training dataset을 가지고서 다시 학습을 최종적으로 시킨다. 그 다음 Testing dataset에 대해서 테스트를 해보게 되면 실제로 이 모형이 어떻게 작동하는가? 잘 작동하는가 잘 작동하지 못하는가에 대한 퍼포먼스를 확인할 수 있다.


2) Bias-Variance Tradeoff
해당 내용은 머신러닝에서의 Bias와 Variance, Bias and Variance (편향과 분산)를 참고하여 보완했습니다.
Supervised Learning에서 정답 하나를 맞추기 위해 컴퓨터는 여러 번의 예측값을 출력하는데,
컴퓨터가 내놓은 예측값의 동태를 묘사하는 표현이 '편향' 과 '분산' 이다. 대체로 아래와 같이 말한다.
예측값들과 정답이 대체로 멀리 떨어져 있으면 결과의 편향(bias)이 높다고 말하고,
예측값들이 자기들끼리 대체로 멀리 흩어져있으면 결과의 분산(variance)이 높다고 말합니다.
활쏘기로 비유를 들어 보자, 과녁의 정중앙(빨간점)이 정답이고 작은 파란 점이 모델의 예측값이다.
- 왼쪽 상단 과녁은
예측값이 정답과 가깝다 => 편향이 낮음
예측값이 서로 몰려 있다 => 분산이 낮음
- 오른쪽 상단 과녁은
예측값이 정답과 가깝다 => 편향이 낮음
예측값이 서로 흩어져 있다 =>분산이 높음
- 왼쪽 하단 과녁은
예측값이 정답과 멀다 => 편향이 높음
예측값이 서로 몰려 있다 => 분산이 낮음
- 오른쪽 하단 과녁은
예측값이 정답과 멀다 => 편향이 높음
예측값이 서로 몰려 있다 => 분산이 낮음

같은 말을 수식으로 보기 위해선 $f(x)$, $\hat{f}(x)$, $E[\hat{f}(x)]$에 대해 먼저 알아야 한다.
- $x$는 데이터를 의미한다. 파란점 하나 하나가 $x$에 해당한다.
- $f(x)$는 데이터 $x$에 대한 실제 정답을 의미한다. 정답은 단 하나이므로 빨간 점에 해당하는 $f(x)$는 하나만 존재한다.
- $\hat{f}(x)$는 모델의 예측값을 의미한다. 모델의 상태(ex. 파라미터)에 따라 다양한 값을 출력한다.
- $E[\hat{f}(x)]$는 $\hat{f}(x)$들의 평균(기댓값, expectation)을 의미한다. 대표 예측값이라 볼 수 있다.
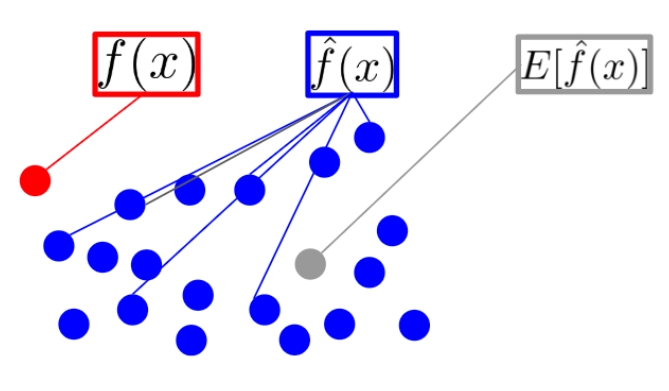
편향(bias)을 수식으로 표현해보자.
편향이란 예측값이 정답가 얼마나 다른가(차이가 있는가, 떨어져 있는가, 멀게 있는가 등)를 표현한다
$f(x)$
$E[\hat{f}(x)]$



Bias라는 거는 뭔가 치우쳐져 있다는 개념이죠. 실제 내가 예측해야 되는 정확한 값이 있는데, 정확한 y 값이 있는데 내가 어떤 예측을 했어요.
y^으로 예측을 했는데 궁극적으로 진짜 아주 정확한 값에서 우리가 예측한 값이 얼마나 떨어져 있는가? 얼마나 치우쳐져 있는가?
그런 걸 측정하는 쉽게 얘기하면 에러가 되겠죠. 오차가 될 거고.
그 다음에 Variance라는 게 있는데 Variance는 뭐냐 하면 여러분이 데이터가 딱 하나 주어져 있지만 사실 그 데이터는 어떤 population, 모집단으로부터 샘플링된 데이터거든요.
그럼 그 샘플링 과정을 추상적으로 생각을 해봐서 내가 가지고 있는 이 데이터는 현재 있는 데이터지만, 모집단은 굉장히 클 거고 사실 여러 종류의 샘플 데이터가 생길 수 있어요.
강아지, 고양이 데이터를 내가 강아지 사진 1,000장, 고양이 사진 1,000장을 모았다고 할지라도
어떻게 내가 샘플링을 하느냐에 따라서 그 고양이 1,000장, 강아지 1,000장의 구성이 계속해서 달라질 수 있겠죠.
그래서 그 과정에서 우리의 모형이 있을 텐데 이 모형이 출력하는, 최종적인 모형이 학습되는 출력하는 최종적인 결과물들도 조금씩 차이를 보이게 되고
그리고 그러한 것들이 어떤 변동성으로 나타나게 되고요.
실질적으로 그런 에러들, 오차, 모형의 오차라고 하는 것이 궁극적으로는 이런 모형이 가지고 있는 편향성과 모형의 변동성으로 표현이 되더라는 게 이론적으로 증명되어 있습니다.
그래서 우리가 모형을 어떻게 학습시킬 때 보게 되면 이 모형의 Complexity, 모형의 복잡도를 우리가 늘려주게 되면 이 bias는 줄어들어요.
그러니까 무슨 말이냐 하면 모형이 복잡하면 복잡할수록 내가 Training data에 대해서 굉장히 잘 설명할 수 있다는 거예요.
미세한 패턴, 미세한 변동까지도 완벽하게 다 학습시킬 수 있다는 거예요.
그런데 그렇게 해놓고 나면 변동성이 너무 큰 거예요. 데이터들이 조금씩만 구성이 달라지게 되더라도 너무 미세하게 모든 걸 다 학습하려고 했기 때문에 변동성이 커지는 거예요.
이론적인 변동성이 커지게 되고, 그것이 궁극적으로는 어떤 오차의 증가, 일반화 오차의 증가로 나타나게 될 수도 있다는 것이고요.
Complexity가 낮으면 Bias는 좀 커져요. 그러니까 무슨 말이냐 하면 너무 간략하게 모형을 만들면 모형이 잘 예측을 못하는 거예요.
실제로 10인데 5, 15, 1, 0, 이런 식으로 예측을 한다는 거죠.
Bias는 커지는데 대신에 Variance는 좀 줄어들어요. 그렇게 Complexity가 줄어들면 새로운 데이터가 오든지 기존의 데이터가 빠지든지 모형이 그렇게 크게 변동이 되지 않습니다.
대신에 Bias가 커졌기 때문에 모형의 오차는 전체적으로 커지게 된다. 일반화 오차가 커지게 된다는 게 이론적으로 알려져 있고요.
그것이 바로 이 Test Sample의 Prediction Error 형태로 나타나는 거예요.
그래서 우리가 찾고 싶은 거는 결국에 가장 적절한, 뭔가 Bias와 Variance가 적합하게 잘 조정이 된 가장 최적의 Prediction Error를 보이는 모형,
가장 낮은 Prediction Error를 보이는 모형을 선택해야 된다.
그리고 그것은 이런 Model Complexity랑 연관이 되어 있고, Model Complexity의 낮고 높음에 따라서
이런 High Bias Low Variance 또는 Low Bias High Variance와 같은 Tradeoff 관계를 잘 조절해야 된다는 것입니다.
그리고 이 Model Complexity를 결정하는 데 키가 되는 거는 바로 이 Hyperparameter다.

3) KNN(K-Nearest Neighbors)
- K : 임의의 숫자, 하이퍼 파라미터오래 전부터 사용되었지만 간단한 데이터에서는 성능이 괜찮고 이해하기 쉽다."두 관측치의 거리가 가까우면 Y도 비슷하다"
이 K-Nearest Neighbors의 키 콘셉트를 들여다보면 이런 개념이에요. 두 관측치의 거리가 가까우면 Y도 Target 또는 그 해당 관측치의 Label도 비슷하다는 거예요.
관측치의 거리랑 가까우면 Target도 비슷하다.
그래서 K개의 주변 관측치의 Class에 대한 majority voting. 말 그대로 다수결이죠.
다수결에 의해서 내 주위에 가까이 있는 그런 관측치들이 누가 있나 한번 살펴보고 그 관측치들의 레이블이 있을 거잖아요.
그럼 그 레이블을 살펴봐서 다수결 투표를 하는 거예요. 다수결 투표를 해서 가장 다수에 속하는 클래스로 분류를 해주는 겁니다.
그래서 굉장히 간단한 그런 모형이라고 할 수 있고요.
그 다음에 이런 거리에 기반을 하기 때문에 Distance-based model
그리고 개별 instance들에 대해서 특성들을 공유할 것이라는 가정을 기반에 두기 때문에 instance-based learning이라고 표현하기도 합니다.
k가 클수록 모델 복잡도가 커질것

다양한 거리 측정 공식.
경우에 따라서 Euclidean Distance가 주로 많이 활용이 되긴 하지만,
측정하는 대상에 대해서 완벽하게 독립적으로 생각을 해서 데이터 공간상에서 완벽하게 독립을 시켜서
그 변수별로 거리를 계산하고자 할 때는 이 Manhattan Distance를 활용하시면 되겠습니다.
범주형 변수는 Dummy Variable로 변환하여 거리 계산


거리 같은 경우에는 이 두 관측치들 사이의 차이, 거리를 어떤 가정을 가지고서 측정할 것인가를 결정해주는 그런 Hyperparameter라고 보시면 되겠어요.

그리고 이 K가 KNN의 Hyperparameter라고 말씀을 드렸는데요.한 가지 더 말씀을 드리면 바로 앞장에서 배운 그 거리를 어떻게 계산할 것인가?Euclidean Distance을 쓸 것인가 아니면 Manhattan을 쓸 것인가 Mankowski를 쓸 것인가.어떠한 거리 측정을 사용할 것인가를 결정하는 것도 일종의 Hyperparameter가 되겠어요.이 모형이 어떻게 작동하는가, 모형의 가정이 무엇인가를 결정해주는 그런 결정 요소잖아요. 거리도 마찬가지로. 그렇기 때문에 거리도 Hyperparameter다.그러니까 이 K가 모형의 복잡도를 결정해주는 Hyperparameter라고 본다면,거리 같은 경우에는 이 두 관측치들 사이의 차이, 거리를 어떤 가정을 가지고서 측정할 것인가를 결정해주는 그런 Hyperparameter라고 보시면 되겠어요.그래서 크게 두 가지 Hyperparameter가 있고, 이 두 개를 잘 결정해줘야 된다.그거는 Validation dataset을 이용해서 테스트를 하면서 결정해주면 된다.그리고 앞에서 얘기한 것처럼 K가 크면 Underfitting, 너무 모형이 단순해지고, K가 작으면 Overfitting. 이렇게 된다.

✅ Lazy Learning Algorithm
‘무슨 Learning Algorithm에 게으르고 부지런한 게 어디 있습니까?’라고 궁금해 하실 수도 있는데,여기서 게으르다고 하는 거는 예를 들어서 선형회귀 같은 경우에는 Training data에 대해서 학습을 시켜놓으면이 β들이 다 결정이 되면서 딱 최종적인 모형 형태가 결정이 되고 실제 input이 되는 데이터가 오기만을 기다리고 있잖아요.먼저 기다리고 있고 input 데이터가 오면 그때 파라미터하고 계산을 통해서 바로 결과물이 나오게 되는데, KNN은 그냥 가만히 있어요.데이터가 있으면 그냥 가만히 있다가 테스팅을 해야 되는 데이터가 오면 그 테스팅 하는 데이터를 기준으로 Training data와의 거리를 구하고 그 다음에 최종적인 결과가 나오죠.그래서 Training data가 전혀 활용되고 있지 않다가 Testing 단계에서 등장을 해서 활용이 되고 계산이 되는 learning 방법이기 때문에 Lazy Learning Algorithm이라고도 불립니다. 물론 advanced된 방법들을 통해서 속도를 가속시킬 수도 있겠지만 실시간적으로 빅데이터에 대해서 K-Nearest Neighbors를 적용하기는 어려운 점이 있을 수 있겠죠.
4) Logistic Regression
Logistic Regression은 그 선형회귀모형의 Classification 버전이라고 생각하시면 될 것 같아요.
다중선형회귀분석. Linear Regression. 그래서 입력변수와 출력변수 간의 선형적인 상관관계가 있다고 가정하고 만든 모형이 Linear Regression이죠.
Logistic Regression은 그럼 뭐냐? Logistic Regression은 이 Y가 범주형 변수, Classification 태스크에 대해서 해결하는 그런 선형 모형은 우리가 Logistic Regression이라고 부릅니다.
그러니까 왜 Logistic이냐? 이 Logistic function이라는 변환 함수를 사용하기 때문에 Logistic Regression이라고 부르게 되었어요.
그러한 Logistic function을 활용하는 Linear Regression 모형이라고 이해하시면 되겠죠.
그러면 우리가 이러한 질문을 해볼 필요가 있어요.
종속변수로 이런 범주형, 1 또는 0만이 나오는데 선형회귀를 여기에 바로 적합을 시키는 게 좋을까? 의미가 있는 것일까? 이렇게 생각을 해볼 필요가 있겠습니다.

그래서 이거를 들여다보면 기본 가정은 이 선형회귀 같은 경우에 x가 커짐에 따라서 Y도 일정하게 쭉 커질 것이라는 가정이죠.
그런데 이 결과를 보면 일정 수준을 넘어가게 되면 이 Y가 계속 이렇게 커지게 돼요.
그런데 우리가 바라는 모형의 특징은 이런 것이 아니거든요.
이런 것이 아니고 x가 커짐에 따라서 어떤 특정 클래스로 굉장히 수렴을 해가고, x가 작아짐에 따라서 어떤 클래스로 분류되는 확률이 줄어들고 하는 그런 패턴을 원하는 것이지
이 Y 값이 무한정 커지는 이런 패턴을 원하는 것은 아닙니다.
그리고 이런 가정의 문제는 x가 커지면 오히려 이 오차, MSE 오차는 굉장히 커지거든요.
그러면 이 모형이 갖고 있는 의미는 뭐냐 하면, 어떤 특정한 나이, 특정한 x1이 있는데 이 특정한 x1이면 정확하게 예측을 한 거고
그렇지 않은 거에 대해서는 ‘예측을 할 수가 없어. 큰 의미가 없어.’
x가 특정 기준점 이상으로 넘어가게 되면 오히려 오차가 커지면서 ‘이거는 예측이 잘 안 되는 거야.’라는 가정인데 이걸 바라는 건 아닙니다.
이 분류 패턴을 찾는다는 건 이거보다는 앞서 말씀드린 것처럼 x가 어떤 기준으로 해서 그거보다 커지게 되면 특정 클래스로 분류될 확률이 굉장히 커지고,
그러니까 확률이라는 개념, 특정 클래스로 분류될 확률, 정도, 이런 개념을 모델링을 해야 되는 거예요.
지금처럼 정확한 숫자 개념이 아니라 분류되는 확률, 분류될 법한 정도를 모델링해야 되기 때문에 이 방식은 적합하지 않다.
그러면 어떻게 해야 되는가? 그래서 Logistic Regression이 필요해지게 된 거예요.

그래서 이 logit 함수, logistic function(sigmoid function)을 이용해서 최종적인 결과물을 분류확률로 나타날 수 있게끔 표현해주는 그런 방법이 필요하다.
여기서는 나이에 따라서 Cancer Diagnosis, 그러니까 암이 걸렸는지 아니면 걸리지 않았는지를 진단하는 거예요.
그래서 암 진단이 되었으면 1, 암이 없다고 진단되었으면 0. 이렇게 두 가지 클래스가 있는 거죠.
그래서 나이에 따라서 암 진단의 확률이 어떻게 달라지는지 그 패턴을 보고 싶은 거예요. 그러니까 이진분류 문제인 거죠.
이 데이터를 plotting을 해보면 나이에 따라서 진단이 됐다, 안 됐다가 있는데 이런 형태가 되고,
앞서 본 것처럼 그냥 선형회귀를 이용하며 의미 없는 패턴을 학습하게 됩니다. 우리 가정에 맞지 않는.

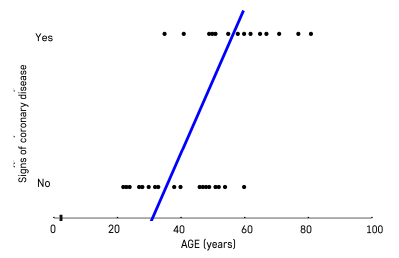
그래서 뭔가 확률 값, 어떤 집단에 속하는지 확률 값을 모델링을 했으면 좋겠고, 일단 그런 실마리를 얻기 위해서 우리가 이 Age group을 나눠보았어요.
Age group을 나눠서 이 나이대에 따라서 몇 명의 사람들이 존재하고 있는지 이 패턴을 본 것이고 그리고 그 Percentage도 한번 계산을 해봤습니다.
그리고 그거를 그래프로 그려보면 대략적으로 이런 형태가 나와요.
그래서 나이에 따라서 암 진단의 분류확률이 점점 커지는 패턴, 그러다가 수렴하는 패턴.
그래서 이렇게 커지다가 100%에 수렴할 수 있는, 작아지면 0%에도 수렴하다가 좀 커지다가 100%에 수렴할 수 있는 이런 형태의 함수가 필요하겠다는 감을 얻을 수 있었고
그런 형태를 모사해줄 수 있는 함수가 바로 이 sigmoid 함수라는 겁니다.




그러면 이 함수의 기본 형태는 원래 이렇게 생겼어요. 1+e^x분의 e^x. 자연로그의 x승.
그리고 이거를 위아래로 e^x승으로 나눠주면 이거는 간단한 대수죠? 단순한 algebra 연산이고.
1+e^-x분의 1승, 이렇게 돼 있는 거고 이 함수를 관찰해보면 x가 0일 때는 2분의 1이고, 입력되는 값이 0일 때 2분의 1이고
x가 -∞로 가게 되면 아래가 무한대로 굉장히 커지기 때문에, 분모가 무한대로 커지기 때문에 0으로 수렴할 거고,
만약에 x가 +∞로 발산을 해가면 어떻게 되죠? 이 부분이 0으로 가기 때문에 1로 수렴하겠죠.
그래서 뭔가 이 결과 값이 확률로 모델링하기가 굉장히 적합한 그런 함수예요. 0부터 1 사이의 값을 예측해주는 함수, 변환해주는 함수.
그래서 이 sigmoid 함수를 사용하게 되었고 그리고 이 sigmoid 함수를 우리 기존에 β0+β1x, 이 함수 있었잖아요. 선형회귀 함수. 여기에 덧씌워주는 거예요.
이 회귀 분석 결과를 sigmoid 함수에 넣어서 출력을 해주게 되면 최종적인 결과가 지금 나이에 따라서 이렇게 증가하다가 수렴하는 이런 함수가 나오게 된다는 것입니다.



기본 가정을 만족하는 함수 형태는 나왔으니까 그 다음에 해야 되는 일은 Loss를 정의하는 거죠. 실제하고 예측된 값하고의 차이.
그래서 그 차이를 구할 수 있는 Loss 함수를 특히 이 분류 문제들에서는, 분류 Classification 태스크들에서는 Cross-Entropy라는 Loss를 많이 사용합니다.


여러분, 보시면 아시겠지만 이 식은 복잡하지만 결국에는 그거예요. 결국에는 실제 클래스.
그러니까 Cancer Diagnosis인지 아니면 Normal Class인지.
이 실제 클래스의 분류확률 값에 로그를 취해서 최종적인 분류 결과가 나오는 거예요
왜냐하면 다른 클래스에 대한 분류확률 값은 다 의미가 없죠. 다 0이 곱해지기 때문에.
그래서 이 Cross-Entropy Loss를 minimize를 해주게 되면 그 말은 무엇이냐?
결국에 지금 마이너스가 붙어 있기 때문에 해당 클래스로 분류될 그 분류확률 값을 굉장히 높여준다. 높여주면 높여줄수록 더 큰 값이 나오게 되는 거죠.
그러면 이 Loss(곱하기 1이 된 것)를 minimize 해주게 되면 실제 클래스로 분류될 확률이 최대화가 되는 그런 β0를 구할 수 있다는 걸 여러분이 캐치하실 수 있을 거예요.

그리고 예제로 만약에 18세인 그런 환자가 있는데 이 환자는 Normal이에요.
실제는 Normal인데 분류기가, Cancer Diagnosis Probability가 0.85다, 굉장히 높다고 분류를 한 거죠. 잘못 분류를 한 거죠.
그럼 어떤 Loss 값이 나오는지 보면, 이 Normal Probability가 되게 낮잖아요. 당연히 이 두 개를 더했을 때 1이 되어야 하기 때문에 상대적으로 낮게 되고,
이게 낮으니까, 실제 클래스로 분류될 확률이 낮으니까 이 Loss 값이 굉장히 커지죠. 상대적으로. 얘네들에 대비해서 굉장히 커지게 돼요.
그래서 결과적으로는 다시 한 번 이거를 minimize 하는 게 결국에는 실제 클래스로 분류될 확률을 키워주는구나. 이거를 다시 한 번 이해를 하실 수 있을 것 같습니다.
'멋쟁이사자처럼 AIS7 > 실습으로 배우는 머신러닝' 카테고리의 다른 글
| [실습으로 배우는 머신러닝] 5. Support Vector Machine (0) | 2022.11.22 |
|---|---|
| [실습으로 배우는 머신러닝] 4. Model Learning with Optimization -최적화와 경사하강법 (1) | 2022.11.22 |
| [실습으로 배우는 머신러닝] 1, 2. 머신러닝 소개 (0) | 2022.11.21 |



댓글