본 내용은 K-MOOC 실습으로 배우는 머신러닝 강의의 내용을 듣고 작성하였습니다.
실습으로 배우는 머신러닝
www.kmooc.kr
5. Support Vector Machine
1) Support Vector Machine
SVM
1995~96년에 처음 제안된 머신러닝 방법론으로 2000년대부터 2010년대까지 널리 사용되어 왔던 방법이다. 딥러닝 이전까지 가장 널리 사용된 방법론이며 여전히 많은 연구가 진행되고 있다.
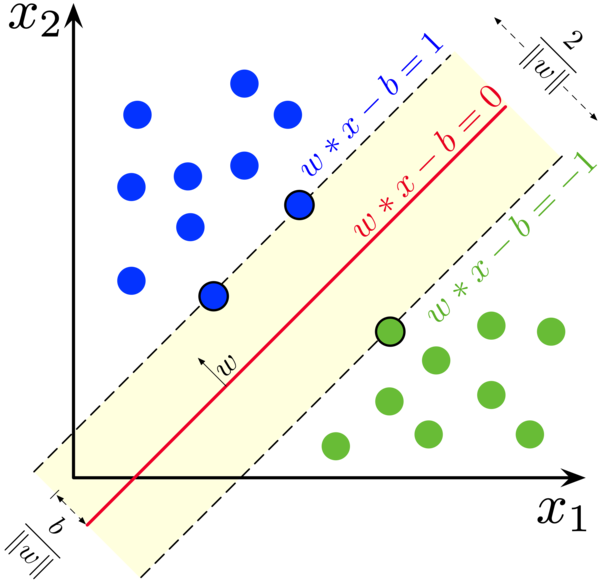
선형이나 비선형 분류 등의 복잡한 분류 문제를 잘 해결하며, 회귀나 이상치 탐색에도 사용 가능하다. 수 천~수 만 개 정도의 중소 규모의 크기를 가진 데이터에 적합하다. 왼쪽 그림처럼 빨간 선으로 데이터를 분류하며 파라미터를 조절해 $x_1$과 $x_2$를 가장 잘 분류할 수 있는 선을 찾는다. 3차원 공간이 되면 오른쪽 그림처럼 평면이 되며, 3차원 이상의 공간에서도 hyperlane이라 불리는 선형적인 분류 함수가 된다.

✅ 딥러닝이 있는데 다른 모델을 알아야 할까?
아직까지도 딥 러닝이 완벽한 그런알고리즘이라고 볼 수는 없습니다.특히 이미지나 음성 인식, 텍스트분석, 그런 분야에서 딥 러닝이두각을 나타내고 있고요.기본적인 정형 데이터 분석이나센서 데이터 분석 그 외에 딥러닝이 커버하지 못하는 영역 그런데이터들이 또 있어요.그래서 그런 부분에 있어서는Support Vector Machine이나 우리가뒤에 배울 Decision Tree, 앙상블모형들, 이런 것들이 더 좋은성능을 보이는 경우도 있습니다. 마스터 알고리즘이란 존재하지 않는다. 문제상황에 적재적소로 사용해야 한다.
SVM의 구조
그러면 어떠한 분류선이, 두 클래스를 가장 잘 나눈 것일까? 처음에 SVM을 제안한 연구자들은 두 클래스 간의 넓이가 가장 큰 분류 경계선을 찾자고 생각했다. 오른쪽 그림의 검은 실선이 최종적인 분류 경계선이라 할때, SVM은 좌우상하의 클래스에 각각 매핑되는 가상적인 분류 경계선(검은 점선)을 그린다. 가상의 분류 경계선은 분류 경계선과 평행하게 존재하며 각각의 클래스를 넘어갈 수 없다. 가상의 분류 경계선이 더이상 넘어오지 못하도록 지지하는 관측치를 support vector라 하며 두 가상 분류선 사이의 거리를 margin이라 한다.
margin이 넓을수록 모델의 융통성이 커진다. 이는 일반화 측면에서 특히나 합리적인데, margin이 만약 되게 작다면 각각의 클래스에서 사소한 이상치가 생겨도 오차가 되어버린다. 그러나 margin이 크기에 각각의 클래스에서 생기는 사소한 이상치는 수용가능한 분류기가 된다.
두 클래스 사이에 가장 넓이가 큰 분류 경계선을 찾기에 Large margin classification이라고도 한다.

SVM은 특성상 스케일이 매우 중요하게 작용한다.
변수의 어떤 스케일에 따른 중요도차이가 나타나지 않고 모두 다골고루 중요성을 가질 수 있게끔스케일링을 해 준 다음에 분류해주게 되면 더 좋은 성능을보이더라는 것이잘 알려져 있습니다.
sklearn을 사용하고 있잖아요.사이킷런을 이용해서프로그래밍하고 있는데 여기에 보면StandardScaler라는 게 있어요.
✅ 스케일링을 왜 해야 할까?
그러니까 웬만하면 대부분의알고리즘들이 스케일링에되게 민감해요.우리가 배웠던 어떤 k-NN 같은경우에도 거리를측정하는 거잖아요, 거리.그러다 보니까 관측치들 간의거리를 측정하는데 특정 변수의스케일이 굉장히 크다고 하면 그변수에 굉장히 치우쳐서거리가 측정되겠죠.그러면 안 될 거고 그렇기 때문에스케일링을 잘해 줘야 하고 SupportVector Machine 같은 경우에도스케일링이 중요하다.
Hard Margin vs. Soft Margin
위에서 배운 Margin의 개념이 Hard Margin이다. 가상의 분류 경계선이 정말로 딱딱한 벽과 같은 존재가 되어, 그 너머로는 관측치가 넘어올 수 없게끔 막기 때문이다. 이는 두 클래스가 하나의 선으로 완벽하게 나뉘는 경우에만 적용 가능하다. 그러나 아래 그림에서는 Hard Margin으로 분류가 되지 않는다. 더욱 문제는, 이런 상황이 극단적인 상황이 아니라 실제 데이터에서 자주 볼 수 있는 상황이라는 것이다. 이를 해결하는 방법이 Soft Margin으로, 일부 샘플들이 가상의 분류 경계선을 일정 수준 넘을 수 있도록 허용하여 문제를 해결한다.
이론적으로 Margin이 최대화되는넓은 그런 분류 경계선을 찾는 것이되게 좋다고 말씀해 드렸죠.그렇기 때문에 이와 같은 상황은그렇게 바람직하지 않은상황이 되겠죠.그래서 이런 것들을 뭔가 타파하기위해서 Outlier의 어떤 효과들이어느 정도 무시되면서 저거는 좀넘어갈 수 있지만 그래도 최종적인Margin이 최대가 되는 이런 어떤분류 경계선을 찾겠다고 하면 SoftMargin 개념을 이용해서모델링을 해야겠습니다.
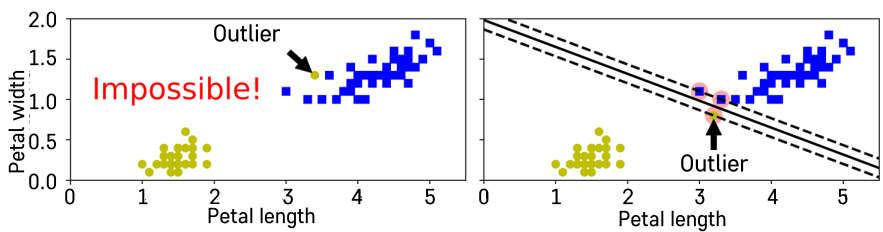
Soft Margin의 정도는 C 패널티 파라미터로 조정한다. 경우에 따라 가상의 벽의 탄성이 강할 때가 좋을수도, 약할 때가 좋을 수도 있다.
그러면 그걸 어떻게 결정하느냐.우리가 계속해서 해 온 것처럼Validation Set가 있어서 우리가탄성 제약을 강하게 주기도 하고약하게 주기도 하고 그러니까 C페널티 파라미터 값을 구체적으로보면 작게 하기도 하고 크게 하기도하면서 Validation Error를보는 거예요.Validation Performance가최대화되는 적절한 C 파라미터 값을골라 주시면 최적의 모형을 학습할수 있게 되는 거겠죠.
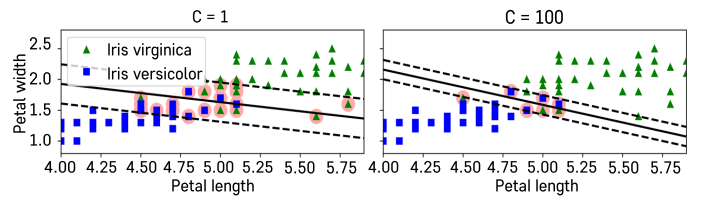
Margin과 Training Error의 Trade-off가 존재함
수학적으로 어떻게 구현될까
일단 우리가 가지고 있는 이수식에서의 목적식, 최적화식에서의목적식은 Margin을 최대화하겠다는목적을 가지고 있다는 것을 일단이해하시면 되겠고요.그다음에 제약식이 있어요.우리가 가지고 있는제약 조건이 뭐였죠?Support Vector Machine 할 때 제약조건이 가상의 분류 경계선들이있는데 이것들 바깥으로 특정클래스의 관측치들이넘어갈 수는 없어.그러니까 모든 관측치들은 가상의Margin을 구성하는 분류 경계선바깥으로 넘어갈 수 없어.파란색은 이쪽으로 넘어올 수 없고빨간색은 이쪽으로 넘어올 수없다는 게 기본 제약이었어요.그것을 정의해 준 거예요.그것을 정의해 준 거고 여기서 보면yi가 나오죠, yi.yi는 무엇이냐면 특정 관측치들에대한 클래스를 부여하는 거거든요.yi는 그래서 +1 또는 -1이에요.그러니까 우리가 2개의 클래스가있죠. 빨간색 아니면 파란색,이렇게 2개의 클래스가 있고요.그다음에 예를 들어서 빨간색은 y가-1로 정의해 주고 파란색은 yi가+1, 이런 식으로 정의되는 겁니다,그렇죠? 이렇게 정의되는 거고그러면 이 제약 조건을 한번이해해 보면 만약에 yi가 +1일 때를가정해 보죠.yi가 +1일 때를 가정해 보면(wTxi+b)≥1, 이게 yi가 +1일 때yi가 -1일 때는 (WTxi+b)는 -1을오른쪽으로 넘겨 주면, 양변에-1을 곱해 주면 -1보다작거나 같다, 이렇게 되겠죠.그래서 여기 가상의 분류 경계선,Margin을 구성하는 가상의 분류경계선들을 식을 어떻게 써놨어요.그래서 wㆍx+b=0, 이걸 만족하는모든 x들은 바로 분류 경계선을구성하는 애들이고요.그다음에 wㆍx+b=+1을 만족하는모든 x들의 집합은 지금 위에보이는 바로 이 Margin을 결정해주는 가상의 분류 경계선을의미하게 됩니다.그리고 -1은 반대로 반대쪽의클래스를 지지해 주는, 막아주는그러한 Margin 분류 경계선이되겠어요. 그래서 이 조건들이되는 거고 만약에 yi가 +1이다.그러면 이 yi가 +1인 관측치들은이 Margin을 구성하는 가상의 분류경계선보다 위쪽에 있어야 한다.더 큰 값을 가져야 한다는 것이고그 말을 생각해 보면 파란색관측치들이 여기 있는 이 가상의분류 경계선보다 아래쪽으로내려올 수 없겠구나, 그렇죠?이 조건을 만족하려면, 이 부등식을만족하려면이라는 것을 알 수 있고그다음에 -1인 상황을 보면wㆍx+b=-1을 만족하는 가상의분류 경계선이 있는데 yi가 -1인애들은 이 가상의 분류 경계선을 또넘어올 수 없겠구나라는 것을 쉽게파악하실 수 있을 거예요.그래서 이 제약 조건은 모든관측치에 대해서 정의되어있습니다, 모든 관측치에 대해서.다시 이 부분을 지우고 써 보면 이제약식은 3 해서 모든 관측치에대해서 다 해당되는그런 내용이 되겠어요.그러니까 우리는 이런 제약을가지고 있는 거죠.넘어올 수 없고 대신에 그 상황에서이 Margin은, 그렇죠?최대를 할 거라는 게 수학적으로정의된 거예요.그리고 그것은 이런 최적화모형으로 정의된 거고요.그러면 이것을 해결하면 우리가원했던 그런 최종적인Support Vector Machine의분류 경계면이 나오게 되겠죠.그러면 이제 이거 어떻게해결합니까? 사실 이걸 해결하는구체적인 Optimization 알고리즘들이있고 또는 Solver들을 이용해서도해결할 수 있어요.그런데 그 부분까지는 좀어드밴스드된 내용이기 때문에구체적인 내용은 다루지는않을게요. 대신에 여러분이꼭 이해하셔야 하는 것은이 수식을 보고서 지금어떤 개념이 어디에 해당되는것이고 그것이 어떻게 구현되어있다 정도만 이해하시면 되겠어요.

2분의1||w||의 제곱이 이게 왜Margin을 maximize하는가에 대해서좀 더 살펴보도록 할게요.그러면 우리가 지금 가상의 분류경계선들이 정의되어 있는 상황에서Margin을 한번 계산해 볼게요,Margin을. 그래서 그 Margin 계산을어떻게 하느냐.일단 임의의 점이 있어요,임의의 점. 임의의 점이 있는데이 임의의 점에서,여기서는 2차원 그런 점이라고생각해 보죠.그런데 여기서 단지 2차원이라고생각했지만 이건 얼마든지 일반화가될 수 있는 그런 개념이에요.앞에 있는 예제에서 2차원으로 되어있기 때문에 그렇긴 하지만얼마든지 x는 d 차원의, 임의의차원에 대해서 정의가 가능한 그런정의라는 것 알아두시면 되겠고일단 좀 쉽게 이해해 보기 위해서임의의 점이 있는데2차원에 있는 점이래요.이 점에서 평면 wx+b-1까지의거리를 구해 보자는 거예요,그렇죠? 그러면 이것은평면과, 그렇죠?이런 임의의 평면이 있고wx+b-1=0을 만족하는 모든 x를모아놓은 평면이 있고 그다음에이런 임의의 점 x가 있으면 이x에서 wx+b-1=0까지의 거리를구해 주는 게 되겠죠.그래서 그 거리라는 것은 이 수직거리일 거예요, 그렇죠?이렇게 수직 거리, 평면에 대해서수선을 내렸을 때 수직 거리가 되는것이고 그다음에 이 수직 거리에대한 공식이 있어요.아마 이 수업을 들으시는 분들중에서 임의의 점에서 평면까지의거리를 구하는 공식을 알고 계시는분도 있을 것 같고 모르시는 분들도있을 수 있는데요.일단 이 공식의 유도 과정은 그렇게어렵지 않기 때문에 여러분이 다른교과서를 보신다든지 아니면 다른어떤 소스를 이용해서 충분히이해하실 수 있을 것 같고 일단저는 공식만 가지고한번 진행해 보겠습니다.일단 이러한 평면이 있을 때 임의의점에서 이 평면까지의 거리 공식이있어요. 거리 공식을 이용해서계산해 보면 지금 이렇게계산할 수 있거든요.그래서 wx+b-1 이 부분 x에다가x´를 대입해 주시고요.그다음에 절댓값을 취하는 거예요.절댓값 취하고 그러고 나서 w의크기, w는 벡터잖아요, 그렇죠?w는 벡터이기 때문에 그 벡터의크기로 이렇게 나눠 주면 됩니다.그러니까 이 공식을 이용하게 되면임의의 점에서 이 해당 평면까지의수직 거리를 계산해 줘요.그래서 이게 기본 거리 공식이되겠고요. 그런데 우리가 구하는Margin이라는 것은 뭐였죠?우리가 구하는 Margin이라는 것은wx+b=0 위의 점에서, 그렇죠?임의의 wx+b=0 위의 점에서wx+b-1=0과 평행하는 그리고분류 경계선이 되는 그 평면에서의거리, 그것을 구해 줘야겠죠,그렇죠? 2차원에다직선을 이용해서 한번그려 보면 이게 분류 경계선이면이게 가상의 분류 경계선이 되겠죠.wx+b=1이 가상의 분류 경계선이될 거고 우리가 알고 싶은 것은 이둘 사이의 거리, 이게 Margin을구성하는 거죠, 그렇죠?그러니까 다른 쪽 Margin도 있긴한데 어쨌든 이것 2개는 평행하고방향만 반대이기 때문에 결국에는이 거리랑 이 거리랑 그다음에 이거리는 같을 거예요.이 거리랑 이 거리는 같을 거기때문에 뭐든지 둘 중의 하나만구해서 maximize를 해 주면 동일한개념을 갖는 식으로 formulation이가능합니다.그렇기 때문에 wx+b-1=0까지의거리만을 한번 구해 볼게요.그러면 일단 이 x″라는 점은 있다.x″이라는 점이 있고 똑같이 이공식에다가 대입해 볼 거예요.그러면 x´ 대신에 x″만 넣어 주면되겠죠, 그렇죠?이게 거리가 될 거고 그런데 여기서중요한 포인트는 뭐냐 하면 이x″이라는 점은 어떤 점이었죠?이 평면 wx+b=0 위에 있는점이잖아요. 그러니까 이 x″는wx″+b=0을 만족하는, 그렇죠?이걸 만족하는 임의의 점인 거예요.이게 임의의 점이긴 임의의 점인데이 평면 위에 있는 임의의 점이기때문에 바로 이 등식을 만족하는그런 x″이 되어야겠다, 그렇죠?그래야 이 개념이 정의가 되는 거죠.그래서 wx″+b=0이겠구나라고생각하시면 되겠고 그러면 여기서보면 이게 이렇게얘가 0으로 소거되겠죠.그리고 절댓값 취해서 계산해 보면w 벡터의 크기분의 1,이렇게 정의가 될 겁니다.그러면 wx+b-1, 우리 분류경계선이 있고 가상의 분류경계선까지의 이 Margin은||w||분의 1이 Margin이구나라는 것알 수 있겠죠.


그리고 wx+b+1=0, 그렇죠?반대쪽까지의 평면, 반대평면까지의 거리까지 고려하면Margin의 길이는 정확히는||w||분의 2가 되겠죠.2배 하는 거, 그렇죠?똑같은 게 2개 있으니까 2배 해주면 되겠고 바로 이 Margin 길이를최대화하세요. Margin 길이를최대화하세요라고 하는 것은어떤 개념이냐면 바로 써 보면maximize 이게 되겠는데 이걸한번 생각해 보면 이 w 벡터의크기가 지금 분모로 들어가있잖아요. 분모로 들어가 있는이 텀을 maximize하고 싶대요.그러면 한번 역으로 생각해 보면이것을 뒤집어서 역수를 취해서minimize 이것을 해 주면, 그렇죠?이 2개는 동치가 되는 거죠, 다시.분모에 있는 것을 고려해서maximize하나 아니면 그걸 분자로놓고 그걸 최소화하나 결과적으로는동일한 일을 하게 되는 거예요.그리고 제곱을 붙이는 것은 이건약간 practical하고 뭔가Optimization 관련해서 테크니컬한부분인데 원래는 w가 예를 들어서w1, w2 이렇게 2개의 변수만 있다고생각해 보죠. 그랬을 때벡터의 크기라는 것은결국에는 이렇게√w1의 제곱+w2의 제곱이잖아요.그런데 Optimization하는 계산과정에서 루트가 있는 것보다는없는 게 더 편해요, 그렇죠?없는 게 더 편하고 제곱을 취해서최소화하나 제곱을 취하지 않고최소화하나 결과적으로최소화한다는 개념은 동일합니다.그리고 최종적인 w1과 w2, w의세부 구성 요소들의실제 최적의 값에 영향을 주지 않는그런 transformation이에요.그런 일관된 transformation이기때문에 우리가 그것을 적용해서 좀더 이것은 practical하게 계산을쉽게 만들어 주는 요소라고생각하시면 되겠어요.어쨌든 중요한 것은 minimize 벡터크기 w 하는 것이 Margin을maximize한다는 이야기구나라는것만 정확히 이해하고 계시면되겠습니다. 그래서 저 수식을해결해 주게 되면 우리가 제약 조건만족하면서 동시에 Margin이최대화되는 그런 분류기를만들 수 있구나, 이렇게이해하시면 되겠어요.

Support Vector Machine 관련해서가장 중요한 개념은 이해하셨고여기서 조금씩 변화들이일어나게 됩니다.여기 기본 Hard Margin 모형은 좀practical하게, flexible하게사용하지 못하는 그런 한계점도있잖아요. 그런 것들을보완해 주기 위해서약간의 변형들이 일어나게 돼요.그러면 그 약간의 변형들을이해해 보도록 할게요.그래서 Hard Margin에 대해서는배웠고 말씀해 드린 것처럼 SoftMargin을 써야지 flexible하게 더좋은 성능을 내는 분류기를 만들 수있다고 말씀해 드렸죠.Soft Margin Optimization을들여다보면 마찬가지로 Margin을최대화하는 부분은 똑같이 있어요.그런데 추가적인 뒤에 텀이 붙죠.추가적인 뒤에 텀이 붙고 여기 보면가상의 분류 경계선을 넘어가지말라고 했던 제약 조건에도약간의 변형이 생겼죠.이 변형이 무엇일까, 이게 바로Soft Margin에서 배운 것처럼약간의 오차를 허용해 주는 대신에페널티를 주는 부분이에요.여기 ξi가 각각의 관측치들에 대한오차라고 생각하시면 되겠어요.그래서 여기 그림에서도 보이는것처럼 만약에 파란색 관측치가여기 넘어가면 안 되는데좀 넘어갔어요.그러면 넘어가면 넘어간 그 양만큼,정도만큼 오차를 부여해 주는거예요. 마찬가지로빨간색에 대해서도 오차를부여해 주는 것이고요.그 개념이 바로 이 제약 조건에담겨 있습니다. 그래서 원래yi(wTxi+b)≥1 이렇게되어 있으면 Hard Margin이었는데이제는 좀 넘어가더라도 그래, 좀넘어갈 수 있지라고 해서 0보다크거나 같은 그런 오차항을 여기다이렇게 빼 주게 되면 이렇게관측치들이 넘어가더라도 좀허용되는 그러한 제약 조건이되겠어요. 그러면 그 제약 조건만있으면 되느냐.그렇게 하면 다 넘어가려고 하겠죠.그래서 앞에서 배운 것처럼 페널티파라미터를 이용해서 조절할 수있는 텀을 목적식에다 넣었어요.그래서 오차들을 다 더해서 지금보면 i는 1부터 N까지 모든 넘어간오차들을 다 더해요.다 더해서 앞에다가Hyper parameter C를 곱해서 정도를조절해 주는 거예요, 그렇죠?그래서 오차가 크게 날 수도 있고작게 날 수도 있는데만약에 C가 크다.100, 1000, 이렇다.그러면 오차가 큰 것을minimize해야 하기 때문에 굉장히오차가 작게끔 분류 경계선이생기게 되겠죠.그리고 만약에 C가 작다, 그렇죠?C가 극단적으로 0이다.그러면 오차를 전혀 고려하지 않고그냥 그런 제약 조건을 전혀고려하지 않는 그러한문제가 될 거고요.그다음에 만약에 다시 한번 써 보면C가 0이면 이건 굉장히 소프트한그런 Classification 모형이 될것이고 그러니까 오차를 고려하지않는 모형이 될 것이고 만약에 C가무한대라고 하면 이것은Hard Margin이 되겠죠.무슨 말이냐면 오차가 조금이라도생기면 목적식을 최소화할 수 없는거예요, 그렇죠?무한대로 발산해 버리기 때문에.그러니까 오차를 전혀 안 생기게끔하는 그런 분류 경계선을 찾으려고하겠죠, 이 최적화 모형이.그래서 이 0과 그다음에 무한대 이둘 사이에서 적절한Hyper parameter Tuning이필요하다는 부분입니다.

그다음에 이렇게 해서 저 문제를해결해 주면 우리가 얻는 것은무엇이냐. 우리가 얻는 것은최종적으로는 이 분류 경계선이에요.이 분류 경계선, 그렇죠?wㆍx+b, 여기는 마이너스라고 되어있는데 일반적으로 마이너스라고해도 되고 플러스라고 해도 되고.그래서 wㆍx+b라고 하는 그런Classification 모형이에요.최종적인 직선 또는 plane, 평면이런 게 될 것이고 그러면 우리는어떻게 하면 되느냐.그다음에 여기다 어떤 관측치를넣는 거예요. 실제로이런 가상의 그런 관측치들이들어왔어요. 관측치가 들어왔으면이 관측치를 대입해서그다음에 만약에 이 관측치가정확히 이 분류 경계선 위에있다고 한다면 그 관측치는wx+b=0을 만족할 것이고 만약에이게 0보다 크다고 하면 이 파란색관측치로서 분류되는 것이고 만약에얘가 0보다 작다고 하면 초록색관측치로 분류되는 것이고 나중에는어쨌든 우리는 wx, w 그리고 b, 그값을 최적화해서 구해 주게 되면거기 식에다가 대입해서 부호만관찰해 주면 되는 거겠죠.그래서 우리가 이런 것들을 어떻게보면 Decision function이다,이렇게 볼 수 있겠고요.그리고 이 Decision function을보게 되면 지금 이게 0 값, 그렇죠?여기가 x축 그리고 y축을 보시면wx+b를 계산한 거예요.그래서 보시면 만약에 이 wx+b가양수가 되면 이쪽 초록색, 음수가되면 여기 파란색에 할당해 주면된다는 것입니다.


2) Nonlinear SVM
일단 기본적인 아이디어 먼저설명해 드릴게요.말씀해 드린 것처럼 Support VectorMachine은 평면으로만 분류해 줘요.평면으로만 분류해 주기 때문에이런 비선형적인 패턴이 있는상황에서는 분류가 쉽지 않습니다.그래서 단순한 예제로 왼쪽에그림을 보시면 파란색하고 그다음에초록색이 있는데 이 둘을 구분하는분류 경계선은 하나의 선으로는절대 안 되겠죠.그래서 이러한 데이터를 이렇게비선형적으로 2차원으로 확장해서그려 주게 되면 x1에 대해서x2=x1의 제곱, 이런 새로운 변수를만들어서 넣어 주면 이렇게데이터가 분포하게 되고 이것들에대해서 이렇게 직선으로 분류해주면 최종적인 분류가 되는형태가 되겠습니다.
SVM은 평면으로만 분류를 해주기 때문에 왼쪽 그림과 같이 비선형적인 패턴이 있는 상황에서는 분류가 쉽지 않다.

끝으로 이동그래서 Nonlinear SVM에 대해서간단한 힌트를 얻어 보았는데요.이어서 구체적으로 어떻게 그러면Nonlinear SVM을 구현하는지좀 보도록 할게요. 아래에 보시면이 그림이 바로 대표적인 어떤Nonlinear SVM을 적용한 결과라고보시면 되겠고요.일단 우리는 크게 두 가지 변수가있어요. x1 그리고 x2,이렇게 두 가지 변수가 있고이 두 변수를 기준으로 해서2개의 클래스가 있는 거예요.파란색 클래스 그리고 초록색클래스. 우리는 이 두 클래스를잘 구분하고 싶은데기존에는 이런 선으로밖에구분이 안 됐잖아요.그래서 이런 앞에서 잠깐 언급된것처럼 직선으로 분류할 수 있는형태로 데이터를 만들어 줄 거예요.다항식 변수들을 추가함으로써,기본 아이디어는 그거예요.다항식 변수를 확장해서 이것들이높은 차원의 공간에서는 선형으로분류될 수 있는 그런 어떤 변수변환 과정을 거쳐서 분류기를 해주게 되면 그것들이 오리지널공간에 오게 되면, 기본 공간에오게 되면 마치 이렇게비선형적으로 분류되는 것과 같은효과를 보이게 되겠다는 것입니다.

그래서 그렇게 다항식의 어떤차수를 높여 주는 방법이 여러가지가 있을 수 있겠죠.우리가 데이터상에서 x1, x2가있는데 나는 이거 2차원으로 늘리고싶다고 하면 기본 변수들이 있고여기다가 +x1의 제곱, x2의 제곱그리고 x3의 제곱, x3은 아니겠죠,x1과 x2의 곱, 이런 식으로 해서이차항 부분을 추가해 줄 수 있고삼차항 부분을 추가하고 싶다.그러면 x1의 3승, x2의 3승, 이런식으로 계속 변수들을 늘려줄 수있는 거예요. 그런데 이런 식으로데이터 차원을 늘리다 보면만약에 높은 차수의 다항식을구성하고 싶다고 하면굉장히 비효율적이 되겠죠.데이터의 어떤 개수도 확 늘어나버리고 굉장히 비효율적으로될 겁니다. 그래서 SVM에서는Kernel이라는 트릭이 있어요.Kernel이라고 하는 기술이 있는데이 부분에 대해서는 사실 더 깊이있게 다루기 위해서는 좀 더 다른차원의 이야기들이 필요합니다.그래서 지금 상황에서는 여러분이이게 뭔가 데이터의 차원을효과적으로 늘려 주는 그런방법이구나 정도로만이해하시면 되겠어요.
그래서 우리가 이 PolynomialKernel이라는 기법을 사용하게 되면오리지널 공간에서 이렇게 막데이터를 늘리지 않아도 효율적으로마치 다항식의 차수를 늘린 것과같은 효과를 내면서도 분류경계선을 찾아주는 방법이 있어요.굉장히 효과적인 방법이겠죠.그래서 그런 Kernel 기법, 이런키워드만 알아두시면 될 것 같은데그걸 활용하시면 되겠고 우리가알아야 하는 것은 차수,dimension을 3차로 할 것인지dimension을 10차로 할 것인지,이런 차수를 조절하고 그다음에적용해 보시면 이렇게비선형적으로, 그렇죠?비선형적으로 잘 구분해 주는 것을보실 수 있게 됩니다.

그다음에 말씀해 드린 것처럼Polynomial Kernel을 이용하게 되면어떤 한정된 차원을 가정하고우리가 적용하는 것이잖아요.그런데 Gaussian RBF Kernel이라는것, Radial Basis Function이라는Kernel, Gaussian Radial BasisFunction이라는 Kernel을 이용하게되면 이거는 무한대 차수를 갖는다항식으로 차원을 확장시키는효과를 가지고 있어요,이 Gaussian Kernel 같은 경우에는.그래서 보통 Gaussian Kernel을굉장히 많이 사용하게 되는데요.그런 어떤 효율적으로 무한대차원으로 확장하는 효과를가지고 있기 때문이에요.그래서 여기서는 우리가 조절해야하는 Hyper parameter는바로 gamma입니다.이 gamma가 커지면 커질수록좀 더 이 gamma가어떤 상황에서는 다양한Variation들이 있을 수 있는데gamma가 커지는 상황에서 좀 더복잡한 패턴을 나타내게끔 그렇게설정되어 있는 구성도 있을 수있고요. 또는 gamma가 작을수록더 복잡한 패턴을 보일 수 있는그런 구성이 있을 수도 있어요.그런데 그 구성과 관련해서는 실제실습 시간에서 들여다보면서sklearn에서 어떻게 조정되는지 그부분은 살펴보도록 하겠습니다.그래서 gamma, 어떤 복잡도를조정하는 Hyper parameter가추가되면서 그것을 조절해서 아래보이는 것처럼 굉장히 단순한 어떤선형부터 출발해서 되게 복잡한,그렇죠? 여기는 삼차 함수 정도되는 형태였는데 지금 보시면 아예이렇게 마치 섬처럼 복잡한 어떤함수의 패턴들을 모델링할 수있게끔 도와주는 그런 기법이다,이렇게 보시면 되겠고 그러면앞에서 봤던 C 페널티 파라미터,그거랑 그다음 이렇게 Kernel의복잡도를 조정하는 파라미터를 잘조절하게 되면 되게 좋은 분류기를얻을 수 있게 되는 거겠죠.

3) SVM Regression
SVM Regression이 필요한 이유는마찬가지로 x랑 y 간의 상관관계가선형적으로, 왼쪽에 나와 있는것처럼 이렇게 선형적으로 잘구성될 수도 있지만 대부분의경우에는 그렇지 않아요.굉장히 복잡한 그런 패턴을 갖는경우들이 있고 그러한 상황들에서되게 유연하게 잘 대처할 수 있는그러한 Regression 모형을 만들기위해서 Support Vector Machine을응용한 그러한 회귀 분석방법이라고 생각하시면 되겠어요.그런데 여기서도 궁극적으로 여러분이해하신 것처럼 어떤 함수를 찾는거예요. 어떤 함수를 찾는 것이고비선형적인 패턴에 대해서는 앞에서배웠던 그런 Kernel 트릭을응용해서 이러한 입력 변수들이고차원의 공간에 간 상황에서고차원의 공간에서는 선형적으로회귀식이 구성되면 그것이 원래 본차원의 공간에서는 비선형적으로구성되는 것과 같은 그런 효과를내는 테크닉을 이용해서 선형뿐만이아니고 비선형적인 패턴을 예측해줄 수 있는 그런 Regression 모형이되겠습니다. 그래서 기본적으로는Classification 모형을잘 이해하시면 되겠고요.SVM Regression은 제가 추가적으로그다음에 알아두시면 좋겠다 정도로소개해 드리는 거니까 한번들어보시면 좋겠고요.기본 아이디어는 그거예요.기본 아이디어는 우리가 x1이 있고y가 있는데 이 둘 사이의 관계를 잘설명하는 직선을 찾는 게 보통Regression의 문제잖아요, 그렇죠?그런데 여기서도 마찬가지로 어떤가상의 분류 경계선과 비슷한 같은가상의 오차 경계선을 주는 거예요,오차 경계선, 그렇죠?이 오차 경계선을 두고 내가 적합한회귀식이 있는데 이 회귀식과 어느정도의 오차를 보이는 것까지는허용하겠지만, 특정 관측치가 이회귀식과 어느 정도의 오차를보이는 건 허용하겠지만 그이상으로 넘어가는 것은허용하지 않는, 그렇죠?그 이상 넘어가는 것은 허용하지않는 그런 회귀식을 찾겠다.그래서 오차에 대한 허용 정도에따라서 지금 왼쪽처럼 좀 많은관측치가 오차를 보이지 못하게되는 그런 상황이 있을 수도 있고오른쪽처럼 많은 관측치들이 오차가나타날 수 있는 그런 상황이될 수도 있어요.이것도 어떤 ε 파라미터와 같은오차의 정도에 대한 페널티를 주는그런 파라미터를 조절해서 적절한식을 찾게 되겠습니다.

그래서 이것은 어떻게Optimization이 구성되겠는가.마찬가지로 이와 같은 Margin을최대화하는, 그렇죠?우리 앞에서 Classification 할 때배운 것처럼 Margin 최대화하는 게똑같이 들어가고요.대신에 여기 Constraints 부분에서실제 y값하고 그다음에 모형이출력한 출력값하고의 오차가 일정수준 이하가 되어야 한다.ε이라고 하는 오차 페널티 이하가되어야 한다는 가정이들어가게 되고요.그다음에 이 ε은 일종의Hyper parameter가 되겠죠.ε은 내가 허용해 줄 수 있는오차의 최대치 정도라고생각하시면 되겠어요.그다음에 여기는Hard Margin이겠죠, 마찬가지로.Hard Margin이고 이런 경우는Soft Margin. Hard Margin은일반적으로 practical하게사용하기 어렵다.그래서 밑에 보이는 것처럼 오차를허용해서 마찬가지로 ξ를 사용해서오차의 범위를 flexible하게변수로서 주고 발생한 오차에대해서 페널티를 부여하는 방식으로식을 구성해서 최종적인 Regression모형을 만드는 그런 형태가되겠습니다.

그다음에Classification 모형과 마찬가지로Kernel 트릭을 이용해서Polynomial Kernel이나 RBF Kernel같은 그런 Kernel 개념을 도입해서지금 보이는 것처럼 이렇게비선형적인 이차 함수 형태를 띠는이러한 함수에 대해서도 잘 적합할수 있는 그런 방법이 되겠습니다.

'멋쟁이사자처럼 AIS7 > 실습으로 배우는 머신러닝' 카테고리의 다른 글
| [실습으로 배우는 머신러닝] 4. Model Learning with Optimization -최적화와 경사하강법 (1) | 2022.11.22 |
|---|---|
| [실습으로 배우는 머신러닝] 3. Classification - KNN과 Logistic Regression + Bias-Variance Tradeoff (0) | 2022.11.21 |
| [실습으로 배우는 머신러닝] 1, 2. 머신러닝 소개 (0) | 2022.11.21 |



댓글